Get To The Point: Summarization with Pointer-Generator Networks
Abigail See, Peter J. Liu, Christopher D. Manning
Abstract
本文提出了一个Sequence-to-Sequence attentional 模型,用于生成文本摘要,数据集使用的 CNN/Daily Mail。此模型思想可用于解决OOV(out of vocabulary)问题。
Our Models
Baseline 模型与 Nallapati et al. (2016)相似,包含Encoder及Decoder,前者为单层双向LSTM,后者为单向LSTM。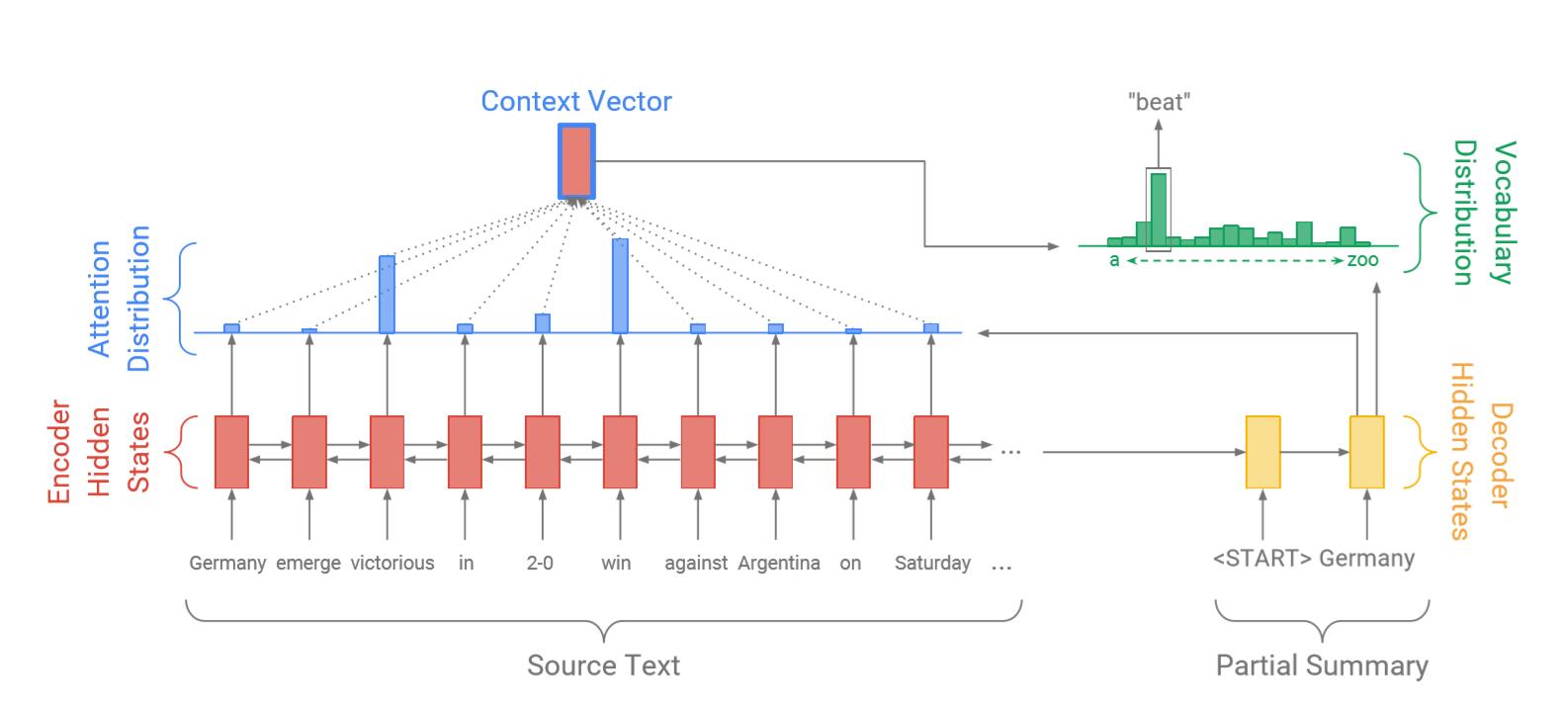
2.1 Sequence-to-sequence attentional model
首先使用Attention机制(Bahdanau et al. (2015)),
$$e_i^t = v^T \text{tanh}(W_h h_i + W_s s_t + b_{attn})$$
$$a^t = softmax(e^t)$$
其中, $V, W_h, W_s, b_{attn}$ 都是学习参数,然后可以计算 上下文向量(context vector) $h^$ :
$$h_t^ = \sum_i a_i^t h_i$$
然后是模型新添加的模块:将上下文向量 $h^{}$ 与decoder隐层状态 $s_t$ 拼接,并经过两层线性层,再使用softmax进行归一化,得到 vocabulary distribution $Pvocab$:
$$P_{vocab} = \text{softmax} (V^\prime (V [s_t, h_t^]+b)+b^\prime)$$
这时候可以得到预测单词 $w$ 最终的分布: $P(w) = P_{vocab}(w)$ 。
在训练时候,每个time-step的 $t$ ,目标单词的 $w_t^$ 的负对数似然估计为:
$$\text{loss}_t = -\log P(w_t^)$$
整个sequence的损失为:
$$\text{loss} = \frac{1}{T}\sum_{t=0}^T \text{loss}_t$$
2.2 Pointer-generator Network
模型的Pointer-generator网络是baseline模型与pointer 模型的结合。其中time-step t 的generation probability $P_{gen} \in [0,1]$ 是由context vector , decoder state, decoder input计算得到的:
$$P_{gen} = \sigma (w_{h^}^T h_t^ + w_s^Ts_t + w_x^Tx_t + b)$$
可以看出, $P_{gen}$是一个软开关,表示通过从 $P_{vocab}$ 中采样来从词汇表中生成(generate)一个单词的概率,或者从输入序列中采样attention $a^t$ 来复制一个单词。我们将原始文档中的所有单词记为 拓展词汇表(extended vocabulary),则其对应的分布(distribution)为:
$$P(w) = p_{gen}P_{vocab}(w) + (1-p_{gen}) \sum_{i:w_i=w} a_i^t$$
如果w是OOV,那么 $P_{vocab}(w)$ 为0,如果w没有出现在源文档中,则公式后者为0。这使得模型能够解决OOV问题。
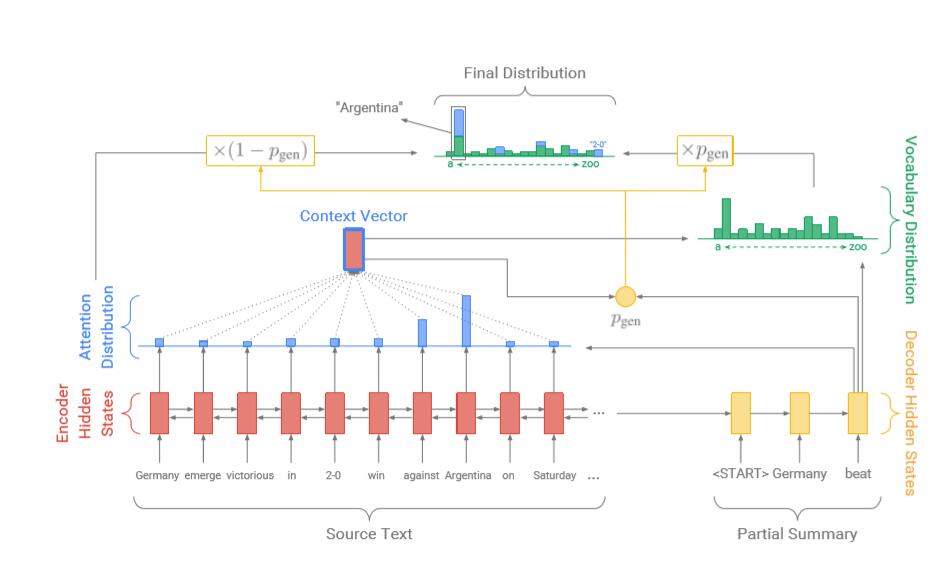
生成一个概率值,将两个distribution进行叠加,从而既可以从源序列中提取单词,也可以从词汇表中选择单词。
2.3 Coverage mechanism
重复是Seq2Seq的常见问题。使用 converage model 来解决这个问题。首先添加一个 converage vector $c^t$ ,它是decoder的之前的time-step的attention distribution和:
$$c^t = \sum_{t\prime = 0} ^{t-1} a^{t^\prime}$$
直觉上,$c^t$ 是源文档单词的分布,表示这些单词受到attention机制覆盖的长远。其中 $c^0$ 是一个零向量。
converage vector是作为attention机制额外的输入:
$$e_i^t = v^T \text{tanh} (W_h h_i + W_s s_t + W_c c_i^t + b)$$
这使Attention能简单的不在重复输出内容。
注意,添加 coverage loss 来惩罚相同位置重复attention 是非常必要的:
$$\text{covloss}_t = \sum_i \text{min}(a_i^t, c_i^t)$$
最后,整体loss为(添加了超参数 $\lambda$ ):
$$\text{loss}_t = -\log P(w_t^*) + \lambda \sum_i min(a_i^t, c_i^t)$$